作者简介：裘江杰（1978-），男，浙江宁波人，中国人民大学哲学院副教授，研究方向为逻辑学、分析哲学。

摘  要：实际因果是一元的还是多元的，是当前因果研究中一个争议的热点。最近，费舍尔基于结构方程模型发展出一种多元论的观点；与其他多元论立场相比较，费舍尔的工作的优点在于使用了形式化方法，使得相关分析清晰而深入。但是，基于新机制主义的框架，本文论证，费舍尔的分类主要是针对群体机制型实际因果进行的，除此之外，还有个体机制型实际因果以及非机制型实际因果，并且对于后两类实际因果，可能需要使用不同于结构方程模型的形式化方法。

关键词：实际因果；结构方程模型；机制；因果多元论

Abstract: Whether actual causation is unary or multivariate is a hot issue in current causality research.  Recently, von Enno Fischer has developed a pluralist theory of actual causation based on structural equation models. The advantage of Fischer's work compared to other pluralist positions is the use of formal methods that make the analysis clear and in-depth.  Based on the framework of new mechanical philosophy, this paper demonstrate that Fisher's classification is mainly aimed at the group mechanical actual causation, and in addition, there are individual mechanical actual causation and non-mechanical actual causation, and for these two kinds of actual causation, formal approach other than the structural equation model is required.

Key Words: Actual Causation; Structural Equation Models; Mechanisms; Causal Pluralism

一 引言

       因果一直是哲学研究中的一个核心概念，对其及相关概念与问题的讨论可以追溯到古希腊时期，自休谟以来，对因果问题的探讨成为哲学的几个重要研究方向之一。

       一般认为，因果概念有一个自然的分类：类型因果与实际因果。前者的例子有“缺碘导致甲状腺功能低下”，而当某个长期摄入碘不足的个体甲出现了甲状腺功能低下的症状时，我们说，这里存在着事件“甲摄入碘不足”与事件“甲甲状腺功能低下”之间的实际的因果关系。类型因果与实际因果有联系但是又相异，有学者认为可将其中一类归约为另一类，如哈尔彭（Joseph Y. Halpern）认为关于类型因果关系的知识得自于对相应的实际因果的概括总结，因此实际因果是更为根本的[1]，也有相反的看法，但是不管如何，对类型因果与实际因果讨论的概念框架通常被认为是不同的。

       作为因果概念的一大子类的实际因果是否是统一的，也就是说，实际因果是一元的还是多元的，则是当前因果研究中争论的一个热点；另一面，上个世纪下半叶以来，形式化方法被路易斯（David Lewis）、 珀尔（Judea Pearl）等一批有着技术背景的学者带入到因果研究中，实际因果研究的这一争论也得到了形式化框架下的考量。

       最近，费舍尔（Enno Fischer）在他的博士论文中发展了一种多元论的观点[2]；这一工作，一方面，由于使用了形式化方法，使得分析相对清晰；但是另一面，由于它基于结构方程统一建模、统一处理；而结构方程模型中的要件，结构方程总表征着某种机制，这使得结构方程形式方法或许只适合于为机制在其中起关键作用的因果关系建模，从而无法处理所有的实际因果，也就是说，费舍尔的分类工作并不完善。因此本文的目标是，在费舍尔的研究的基础上，推进对实际因果的分类工作。更具体的，本文的安排如下：在第二节我们会梳理当前对实际因果研究的基本情况；在第三节介绍费舍尔的多元论观点及其论证；在第四节分析结构方程在讨论实际因果分类问题上的局限性；在第五节中给出实际因果一个新的分类。

二 实际因果

       按照当代因果问题研究的一般看法，我们的因果概念有两个子类：类型因果（Type Causation）与实际因果（Actual Causation）。类型因果知识表述一般性的规律、原理，而实际因果则是关于实际发生的具体的事件的[1]。

       并非所有的学者都认可实际因果关系的因果关联项是事件。保罗（L. A. Paul）认为实际因果关系的因果关联项应该是性质实例（Property Instances），最近，刘牧也为这一观点做了辩护[3],[4]。我们认为这两个看起来相互冲突的观点在实际因果多元论的框架下是相容的：在多元论的框架下，存在着不同种类的实际因果，其中有些类型的实际因果，事件是它们的因果关联项，而另一些实际因果的因果关联项则是性质实例，我们会在第五节再回到这个问题上，不过在接下来的梳理中，我们先把注意力集中在以事件为因果关联项的实际因果上，因为它们是讨论、分析实际因果关系时最常遇到的。

       即使把因果关联项限制到事件上，对于实际因果到底是怎样的，仍然存在着争议。主流的看法是，世界由事件之流组成，我们总是在具体的情景里，试图去确定因果关系，也就是在这个事件之流中“抓取”几个已经发生的事件，将其中之一认定为结果，而将其余的认定为原因，这种实际因果关系的认定，使得我们可以对那个作为结果的事件的发生做出一定的理解与解释，进而可以采取补救，或者加强的措施，做出相应的奖励或者处罚的决策。这种主流观点下的实际因果关系的选取充斥了我们日常的生活与工作，我们无时无刻不在与这样的实际因果关系打着交道。

       对于这种主流观点下的实际因果关系的探求，有着这样的一般模式：确定一个作为结果的事件，然后沿着时间线回溯，明确带来（bringing about）该结果的诸原因，希区考克（Christopher Hitchcock）称之为回溯式（backward-looking）的实际因果关系[5]。

       对于这种主流观点，有着两方面的反对意见。

       其一是所谓的来自密尔的挑战（Mill’s Challenge）[2]p.25，可以用一个简单的例子来说明密尔的挑战指向的是什么问题：在通常情况下，划一根火柴，火柴点着了，我们会说“划火柴”是“火柴点着”的原因，而把有足够的氧气当作背景。密尔认为，把一些事件当作原因而只把其他相关的事件作为背景，是人为的，进而，所有在 “带来”结果事件中发挥作用的事件都应该算作为该结果的原因。谢弗（Jonathan Schaffer）把这种看法称为因果的平等主义观点（Egalitarian conception of causation）[6]。然而，我们认为，平等主义观点的背后是对一种脱离人类实践的纯粹的本体论的立场的坚持，一旦启动这种“去人类实践”，那么其将无法合理地停留在任何中间的位置，而只能导向它的极限形态，而在极限形态里所呈现的，要么是无穷无尽的无比琐碎纠缠在一起的事件，要么是统合为一庞大无外的事件，不论是哪一种情况，实质上都无因果可言。因此我们将不采纳这一平等主义的立场。当然这时，如何将原因与背景条件分离开来，即所谓的原因挑选问题，成为真正需要面对的问题，但是这同时也提供给了多元论一个侧面的线索，正是因为客观上有着多种类的实际因果，才致使无法给以一刀切的统一标准，从而使挑选问题变得如此困难。

       第二个反对意见认为，实际因果可以涉及未来的事件。费舍尔认为，将未来的事件容纳到实际因果中来，“可以使我们从操控（intervention）的角度理解我们对实际因果的兴趣”[2]p.13。操控主义（Interventionism）是因果的反事实理论的一个主要版本，我们也认同这一理论框架。然而我们认为，费舍尔的这一看法存在着两方面的问题。首先，反事实理论本身并不需要在“反事实设置”时引入未来的事件，不管是路易斯的基于反事实条件句语义学的处理，还是莫德林（T. Maudlin）的方案都不以未来的事件作为必要的构件 [7],[8]。其次，费舍尔或许是由于混淆了因果、因果解释与因果推断，而提出这一观点的。简单说，我们引入因果、因果解释的目的是希望呈现客观的因果关系，而因果推断则主要使用概率统计的方法来研究因果问题，特别的，近二十年来，因果推断的主要成就是结合统计学与计算机科学，发展出了几类重要的方法与框架。这样，一方面，可以使用因果推断方法预测未来的事件，另一方面，我们对实际因果的探求也可以使用各种因果推断方法，因此，以因果推断为中介，因果、因果解释联系到了未来的事件。但是，实际因果探究本质上是在相对宏观的尺度上，对已经发生的结果，整理出“带来”此结果的原因，因此其间涉及到的都应该是已发生的，这在逻辑上已经排除了未来的事件。

       这里的细微之处在于，在经济学等领域中，对于相关的实际因果的研究不仅仅以确定因果关系为最终目标，这些研究试图找到的是因果现象背后的机制或者不变性，这种不变性可能在不算短的未来也会是维持着的 [9]。我们也认为这样一大类研究中所探索的也属于实际因果，但是此间的要点仍然不在于涉及到未来，而是时空尺度的放大以及由此带来的对实际因果概念的拓展，概言之，涉及到对未来的预测只能是属于因果推断，这是认识论性质的工作，而要容纳具有一定稳定性的大时空尺度的实际因果则需要改变以往的关于实际因果的刻板看法，这也在某种意义上指向了实际因果的多元论。在这一点上，费舍尔的直觉有其合理性，只是他将这种直觉落实到未来的事件上才产生了偏差。

       综上，我们认为，在实际因果的相关研究中，我们真正关心的是已经发生的事件之间的因果关系，以及，在一些情况下，讨论因果现象背后的机制或者不变性。在这一界定下，实际因果所容纳的范围已经相当广，下面举三个例子说明这一广泛性。

       例子1   1986年，美国挑战者号航天飞机失事，物理学家费曼通过著名的O型环实验，揭示了挑战者号航天飞机失事的根本原因--低温下橡胶失去弹性。在这里，事件“挑战者号的部件O型橡胶环失去弹性”是事件“挑战者号失事”的原因。我们的日常生活中充满了这种单次性的因果关系，而当我们提到实际因果这个概念时，首先想到的，很可能是这样的因果关系的例子。

       例子2  有两只鸽子苏菲与爱丽丝，苏菲被训练得去啄一个物体当且仅当那个物体是红色的，爱丽丝则被训练得去啄一个物体当且仅当那个物体是猩红色的。假设在一个情景里，苏菲与爱丽丝都看到一个猩红的物体，并啄了它。在心智因果与随附因果的讨论中，会得出这样的实际因果关系的论断：是由于这个物体是红色的导致苏菲啄了此物；但是，是由于这个物体是猩红色的导致爱丽丝啄了此物。

       例子3[2]p61  印度曾经发生过多次严重的饥荒，许多人会把饥荒的原因归为当时恶劣的气候引发的粮食歉收，而世界粮食署指出，印度饥荒的真正原因是印度政府没有建立起合理的粮食储备体系。在经济与社会学中研究的，通常是这种涉及到大时空尺度的实际因果关系。

       这三个都是实际因果的例子，因为它们都是关于已经发生的事件的原因的确定，但是直觉上它们是不同的，实际因果的这种广泛性，一方面反映了对实际因果的哲学反思的意义与重要性，另一方面也提示我们，实际因果应该是多种类的，进而，对它们的形式化分析或许需要采用不同的方案。

       在接下来的一节，我们将梳理费舍尔对实际因果多元论的论证。

三  费舍尔的实际因果多元论

       费舍尔的多元论的“假想敌”是哈尔彭及其合作者基于结构方程模型提出的对于实际因果的各种统一定义方案[2]p115，不过，费舍尔的工作本身也基于同样的形式模型，因此我们下面先简单介绍关于结构方程模型的基本概念以及哈尔彭等学者处理方案的最新版本。

       一个结构方程模型ℳ是一个两元组< ?, ℰ > ，其中?是变元集，每个变元代表一个性质（这时该变元取二值）或者一个事件类（这时该变元取多值），?为两个不相交的子部分 U与 V 的并（? =U⊔V），其中 U 是所有外生变元（exogenous variables）的集合，而 V 则包含了所有的内生变元（endogenous variables）；变元间之所以有这种“内外”之别，其原因在于，一个结构方程模型不可能把所有的性质或者事件类都容纳进来，那样即不现实，也无必要，但是如此一来，就必然会有一些变元，它们受到了模型中并未表示出来的因素的影响，这样的变元，我们称其是外生的。

       ℰ是一个由若干个结构方程组成的集合，对于每个内生变元?，有一个相应的函数??在ℰ中，函数??指定了?对于它的父变元的依赖方式，它外延化地“打包”了?的父变元的取值对?的取值的影响。一些学者认为结构方程编码了变量间的反事实依赖关系，另有一些学者认为结构方程表示的是机制；比如，哈尔彭认为“结构方程可以使我们决定，当一些（实际）事件不同于它们实际时，情况会怎样”[1]p14，这种看法又把结构方程理解为编码了变量间的反事实依赖关系；费舍尔也继承了这一看法[2]p.75，p.79；而珀尔则认为结构方程具有模块化的不变性[10]p.223，这种不变性正是机制的体现；哈尔彭与希区考克称“结构方程可以看作是对世界的客观特征的描述”[11]，似乎与珀尔的想法接近。不过不管是哪种理解，结构方程总是反映着变元之间的某种恒常连接性，在第四节中我们会由此说明，结构方程的这一特性，使得结构方程形式模型方法在讨论实际因果分类问题上存在着根本的局限性。

       哈尔彭与其合作者，在干预主义的框架下，基于结构方程模型，试图给出实际因果统一的定义，“一揽子”理清所有的实际因果的“面貌”，但是由于碰到了各种反例与困难，他们给出了多个不同的定义，费舍尔梳理出了最新近的版本[2]p.84，结合希区考克给出的术语[12]，我们只介绍这一版本的定义。

实际因果的 HP 定义

       设ℳ是一个结构方程模型，当ℳ的所有的外生变元的值确定时，ℳ中的所有的变元的值也将固定，用?⃗表示赋予相应的外生变元相应的值，记为(ℳ, ?⃗)，并称之为一个情景。称事件? = ?在情景(ℳ, ?⃗)中是事件? = ?的实际原因，如果下面三个条件同时成立：

（1） ?与?是不同的变元；

（2） 事件? = ?与事件? = ?都在该情景中实际发生；

（3） 存在?的两个不相交的子集Γ与Δ，使得? ∈ Γ，并且

（3. ?）Γ中某些变元取反事实值而Δ中变元都取实际值时，? ≠ ?；

（3. ?）无Γ的非空真子集Σ，Σ满足条件（3. ?）。

       这三个条件中，（1）与（2）比较容易理解，首先，事件不会是它自身的原因，因此需要有（1）；其次，实际因果讨论的本就是实际发生的事件之间的因果关系，因此需要有（2）。第三个条件看上去复杂，但是其背后的直观仍然是清晰的：一个结果事件的发生总是由包括原因与背景条件在内的多因素组合带来的；（3. ?）的意思是，只要这多因素组合的情况发生变化了，那么结果事件就不再发生了；而（3. ?）则表明这多因素组合缺一不可。

       这个简单的定义可以形式化，进而解释许多常见的实际因果关系，同时也能回应一些因果理论所面对的反例[12]，但是费舍尔认为这个定义对所有的原因“一视同仁”，而这种同等地位的处理会与我们在一些因果情景里的直觉相冲突，费舍尔在他的论文中给出了三个例子[2]，下面介绍其中一个例子。

       例子 4[1]p.100  灯泡与双联双控开关

       一个电路里串联着电源、灯泡 C 与一个双联双控开关，相互隔离的 A 和 B 分别控制一个开关。A 先决定是将她控制的开关按向左还是向右并告知 B 她的动作，然后 B 按开关。两个开关位置相同时，电路通，灯亮。在这个具体的情景里，B 想使灯亮，因此她把开关按到和 A 一样的位置，灯亮了。

       用结构方程模型来表示，这里有三个变元 A、B 与 C，A=1 表示 A 将开关按向左，A=0表示 A 将开关按向右；B=1 表示 B 将开关按向左，B=0 表示 B 将开关按向右；C=1 表示灯亮，C=0 表示灯灭；相应的结构方程模型如下图所示[2]p.122②，那么在这个具体的情景里实际发生的事件分别是 A=1、B=1、C=1。

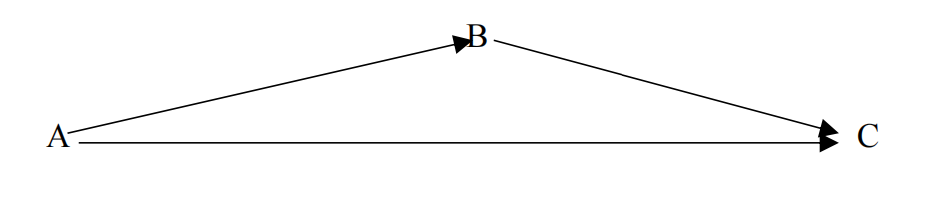
图 1 灯泡与双联双控开关

       根据 HP 定义，取Γ = {A, B}，取Δ为空集，那么可得 A=1 与 B=1 都是 C=1 的原因；然而我们对 A=1 是否可以算作为 C=1 的原因则有争议，有人会认为 A=1 是条件而不是原因，另一面，即便那些认为 A=1 是 C=1 的原因的人也会同意，都作为原因，A=1 与 B=1 不具有同等的地位。由此，费舍尔认为，HP 定义存在着不足，需要对原因进行分类，以解释我们的直觉。

       费舍尔认为，实际因果中有三类原因：全因（Total Cause）、支持因（Contributing Cause）

       以及路径变因（Path-changing Cause），由于篇幅的限制，我们将只介绍其中的两类，全因与路径变因。全因（Total Actual Cause）[2]p.127称事件? = ?在情景(ℳ, ?⃗)中是事件? = ?的全因，如果下面三个条件同时成立：

（1） ?与?是不同的变元；

（2） 事件? = ?与事件? = ?都在情景中实际发生；

（3） 有不同于?的?′，使得在世界(ℳ, ?⃗)中让? = ?′发生后，事件? = ?不再发生。

       费舍尔指出，这个定义能帮助我们区分“灯泡与双联双控开关”的两个事件 A=1 与 B=1的因果地位：

       首先，B=1 是 C=1 的全因，因为当取 B=0 时，由于双联双控开关的两个开关不在同一位置，电路将被切断，进而灯会灭。定义的三个条件都成立，因此 B=1 是 C=1 的全因。

       其次，A=1 不是 C=1 的全因，因为当取 A=0 时，A 会告诉 B 她将开关按向了右（A=0），那么根据例子中的设定，B 也会将开关按向右（B=0），那么电路仍通，C=1 保持不变，因此定义中的条件（3）不成立，因此 A=1 不是 C=1 的全因。

       另一面，费舍尔认为，在这个例子中，A=1 是 C=1 的一个路径变因。

       路径变因（Path-changing Actual Cause）[2]p.127称事件? = ?在情景(ℳ, ?⃗)中是事件? = ?的路径变因，如果下面三个条件同时成立：

（1） ?与?是不同的变元；

（2） 事件? = ?与事件? = ?都在情景中实际发生；

（3） 有?的一个子集Γ，以及不同于?的?′，使得在情景(ℳ, ?⃗)中让Γ中的每个变元都保持实际值，并且使? = ?′发生后，事件? = ?不再发生。

       根据这个定义，可以判定 A=1 是 C=1 的路径变因：取Γ = {B}，在固定 B=1 下，取 A=0将得 C=0，因此定义的条件（3）成立。

       不难验证，所有的全因都会是路径变因，尽管上面的例子表明，存在着非全因的路径变因，但是费舍尔的分类并不是互斥的，不过在讨论费舍尔的分类的进一步的问题之前，我们先指出费舍尔处理的一个优点，这一点在费舍尔的论文中似乎未强调。

       对照上面对全因和路径变因的定义，容易让我们有这样的印象，就是，根据费舍尔的定义，路径变因里能作为全因的似乎是处于时间中较晚出现的实际原因，下面的例子将说明情况并非如此，这将加深我们对费舍尔的定义的理解。

       例子 5  灯泡与双联双控开关的变化版本

       基本设定与例子 4 相同，除了一点，就是 A 与 B 合作使灯点亮，但是 B 出于某些原因，会故意不与 A 配合而使任务失败，而 A 知晓了 B 的心思，因此尽管 A 将开关按向左，但是跟 B 说她按向了右，而 B 为了捣乱，将开关按向了左，于是灯亮了。

       在这个例子中，A=1 发生在 B=1 之前，但是根据费舍尔的定义可以分析判定，A=1 是C=1 的全因，而 B=1 只是 C=1 的路径变因而非全因。因此费舍尔的定义尽管相对简单，仍然能够帮我们分析、辨析许多实际因果现象；然而费舍尔的分类及其相应的形式定义都是基于结构方程模型进行的，这使得他没能注意到实际因果的层次比他所呈现的还要丰富，在下一节里我们会指出其局限性。

四 再论结构方程模型

       在上一节中我们介绍了费舍尔对实际因果的分类，他把实际因果分为全因、路径变因与支持因这三类，它们之间并不是互斥的，而是处于一种递进的关系。费舍尔的工作使得我们对实际因果可以有更加细致的理解，然而从“分类”的定义本身来看，由于这几个概念是递进而非互斥的关系，因此在严格的意义上，这一工作不能算是真正的分类，不过这一点并不是费舍尔的工作的真正的问题，真正的问题出在这一工作整个都是基于结构方程形式模型方法进行的，而结构方程模型中的主要构成要件，结构方程的特性使得这种模型能够处理的实际因果的种类受到了限制，这使得基于其的分类工作不可避免存在着先天不足的问题。

       我们在上一节介绍结构方程模型时曾经指出目前存在着对结构方程的两种理解，其一认为，结构方程编码了事件间的反事实依赖关系，另一则相信，结构方程是对机制的反映。

       在一般的原因研究中，存在着两类被认为是对立的因果理论，反事实理论与机制理论，一些学者认为反事实理论更加基本[14],[15]，另外一些学者则认为机制理论是更加基本的[16]，还有学者，比如前面已提到的哈尔则认为存在着两种因果关系，其一是产生（produce），其二是依赖（dependence），前者对应着机制，后者即反事实依赖，因此需要不同的因果理论分别进行处理[17]。

       不过，对结构方程模型中的结构方程的这两种理解并不简单与这两类理论相对应，事实上，就如前面已经指出的，基于结构方程模型发展出来的因果理论大多属于所谓的干预主义方案，特别的，费舍尔与哈尔彭及其合作者提出的因果理论也属于干预主义范畴，而干预主义理论是反事实理论的一种变种。干预主义理论的主要提出者都是科学家或者科学哲学学者，与传统的反事实理论的提出者路易斯不同，他们在本体论上是相对朴素的，即使是作为哲学家的伍德瓦德，也未预设可能世界这样的事物，伍德瓦德的反事实干预，更多地属于语义学或者认识论层面[18]p138。

       哈尔彭认为结构方程编码了变量间的反事实依赖关系[1]p14，但是他没有讨论结构方程是否对应着机制；结构方程形式模型方法的另一位主要研究者珀尔则认为，在讨论实际因果时，模型中的结构方程表示的是机制[10]p310，不过他也并未进一步澄清机制这一概念，我们会在第五节，借助新机制主义哲学所提供的框架，给出进一步的说明，在这里，则暂时先依据对机制的朴素理解讨论前面提到的结构方程的关键特性，这一特性使得费舍尔的分类工作存在着缺陷。

       一方面，如果我们象珀尔那样，认为结构方程表示着机制，那么结构方程总在某种程度上反映着实在，尽管在不少的时候，我们可能只能完成“拯救现象”的工作，这意味着，在总结出结构方程时，即使只是对以往经验数据的纯拟合，它们也在一定程度上表征着其背后的机制。而机制总是具有着至少是局部的普遍性，因此结构方程反映了相关事物的某种恒常联结性。

       另一面，如果悬搁结构方程对机制的表征，结构方程是否仍然反映了恒常联结性？答案是肯定的。在这种情况下，结构方程编码了反事实依赖关系，伍德瓦德称，形如? =??(?1, ⋯ ,??)的结构方程“描述了?的取值如何随着?1, ⋯ ,??的取值的确定而确定”[19]p43，也就是说，?的取值情况与?1, ⋯ ,??的取值情况之间存在着恒常联结性。

       由此而来，我们可以认为，结构方程总是凝结了关于事物恒常联结性的信息；即使那些只是面向“拯救现象”的对以往经验数据的纯拟合而得到的结构方程，仍然可以认为至少在非常稀薄的意义上承载了恒常联结性的信息。

       同时，正是由于这类模型的这种特性使得它们在因果研究中得到了关注与重视；它们被广泛的使用于实际因果的各种讨论中，之所以如此的原因在于，因果研究中的两个目标，预测与干预都依赖对这种恒常联结性的分析与判断，这使得具有这一特性的结构方程模型自然而然进入到研究者的视野中。

       不可否认，对于结构方程模型的使用确实加深了我们对因果、实际因果等概念的理解，然而，对它们的过度关注也会遮蔽我们的视野，特别的，费舍尔对实际因果的分类这一工作的局限性正是因为这一分类工作完全是基于结构方程模型进行的。下面我们通过一个例子说明这种局限性。

       例子6  小明迟到

       小明性格慢，做事拖拉，开会经常迟到，被领导多次批评。某天上午，一次重要的会议即将开始，仍然未见小明身影，领导无奈地摇头：“小明这个小伙子各方面都不错，但是太拖拉了，今天又迟到了”；几分钟后，小明满头大汗急匆匆跑进了会议室，边找他的位子，边向大家道歉：“各位抱歉，我知道今天会议很重要，提早半小时就出门了，还打出租车来的，这个时间段以往都不堵车，结果今天车堵了一路，不巧路上也没有共享单车，我是跑着来的，还是迟到了。”

       在这个例子中，我们或许可以把“做事拖拉”与“迟到”理解为类似路易斯意义上的共相（universals）或者属性[20]，如果小明的迟到确实是由于小明做事拖拉导致的，那么由于“小明做事拖拉”与“小明迟到”存在着某种恒常性联结，则小明的这次迟到的原因，是 “小明做事拖拉”；然而，在这一情景里，小明实际上克服了拖延的坏习惯，直观上，我们会认为，其最主要的原因应该是偶发的“堵车”，这里的原因与结果之间并无恒常联结性。

       在我们的日常生活中，存在着大量的这种偶然的因果关系，在这些实际因果事件中，原因与结果之间皆无恒常联结性可言，因此将恒常联结性作为实质性组成部分的结构方程模型或许在根本上就无法成为分析这些实际因果的合适的形式化模型，换言之，如果我们只是基于结构方程模型进行实际因果的分类工作，那么一定会有大量的实际因果遗漏在我们的视野之外的，自然费舍尔的工作也不能避免这一问题，因此，在认可费舍尔为我们带来洞见的基础上，我们需要考虑把更多的实际因果容纳进来，然后再进行分类，这一工作将在下一节进行。

五 新的实际因果的分类

       上个世纪末发展起来的新机制主义哲学（New Mechanical Philosophy）正好为我们的讨论提供了合适的概念框架[21],[22],[23]。

       在新机制主义者看来，以生物学为代表的学科领域里研究的主要对象是各种具体的系统，这些系统由组件（entities）有机地组合在一起，进而具有可预测的行为（activities），他们用机制（mechanism）指称这样的系统。

       结构方程里对应的恒常联结性是一种普遍性，但是它们又不同于象物理学这样的基础科学中给出的规律的普遍性，而是相对具体的时空范围内的某种规律性，从新机制主义哲学的角度来看，这种一定的时空范围里的规律性是对具有某种稳定性的系统的性状的反映，这些系统是具体的，换言之，结构方程对应着机制，因此，结构方程模型能够处理的实际因果其关键是其中存在着这样的机制，比如前面所举的例子3就属于此类实际因果。然而，如例子6所示，并非所有的实际因果都是机制性的，因此我们首先可以把实际因果分为机制型实际因果与非机制型实际因果。

       根据机制这个概念对实际因果作了这一分类以后，有一点首先需要澄清，那就是非机制型实际因果并不意味着对机制的完全排斥。

       按照朴素的看法，世界并非只是由不断发生的事件组成的“马赛克”，也就是说，我们认为接续发生着的事件是由机制“勾连”在一起的，这一点对非机制型实际因果也成立，然而在这类实际因果关系中，相应的机制起的是支持性作用，而非关键构成要件，下面的例子可以使我们看出这里的实质所在。

       例子7

       在一个常年高温的沙漠里，一个富豪拥有一庞大的花园，花园里种植了大量珍贵的花卉、草木，其中有一株花A异常娇贵，每一天必须浇够四次水，否则第二天就会枯萎；花园由一位尽责的园丁B料理着，B几乎未出过差错，但是某天，B疏漏了对A的浇灌，第二天A就枯萎了。

       在这个例子中，当地常年高温的气候，A的生物学特性甚至庞大繁杂的花园都可以认为是“支持”了这个例子里的实际因果关系的机制，然而，除了有平等主义倾向的学者外，大部分人都不会认为这些是导致A枯萎的原因，在直观上，我们会认为，是B的疏漏导致了A的枯萎；并且，我们也认同，事件“B疏漏对A的浇灌”与事件“A枯萎”之间并无恒常的联结性，而那些机制只是起到支持性的作用，因此这个因果关系里并无具体的机制作为关键构成要件。

       这个例子里演示的实际上是在因果研究中颇受关注的缺失因果；我们认为，包括这种缺失因果在内的许多实际因果都无具体的机制作为关键要件，因此尽管其中必然有机制起支持作用，它们仍然都属于非机制型实际因果，进而，结构方程模型不适合于对它们建模。

       这样，一个实际因果关系属于非机制型实际因果与机制型实际因果中哪一类的关键是，其中是否有机制作为关键构成要件。根据我们前面对结构方程模型的分析，我们认为结构方程模型不适宜于作为非机制型实际因果的形式模型，而路易斯提出的神经元图或许是更加合适的形式模型，由于篇幅的关系，不在这里展开，我们已另文做了讨论。

       接下来一个自然的问题是，结构方程模型是否可以用来处理所有的机制型实际因果？我们也不认为可以给予肯定的回答，换言之，机制型实际因果内部仍然可以进行分类。

       让我们回看在第二部分提出的两个例子，例子2与例子3：从机制的概念框架来看，这两个例子显示的都是机制型实际因果，然而两者仍有区别，在例子2中的鸽子苏菲与爱丽丝都是作为整体的机制系统出现的，相应的因果关系是由于系统的特性而产生的，我们可以使用，比如（适当调整后的）因果的反事实理论来分析，确定其中的因果关系，而不必“解剖”系统，对系统的部件及它们的组合做相应的探究；另一面，尽管例子3也是机制型实际因果，但是与例子2不同的是，其中的机制系统有着更大的时空跨度，有更加复杂的组件以及组件的组合，特别的，要准确的确定其中的实际因果关系需要对系统的构成本身进行实质性的分析，这使得我们需要使用变元把相应的组件以及其可能的取值表示出来，也就是说，我们需要“深入”到系统内部才能分析清楚相应的因果关系。从上面的讨论中可以看出，这两个例子的差别在于，在确定因果关系时，前者的系统是作为整体进行讨论的，而后者则需要分拆系统，这种差别的实质或许在于系统的耦合性，前者由于是高度耦合的，因此是真正单一的机制系统，而后者则是大量的更小的机制系统的低耦合度的组合，因此这两者在可以使用的分析手段上存在着差别。更加一般的，我们可以根据系统的耦合程度，将机制型实际因果进一步分类为个体机制型实际因果与群体机制型实际因果。

       在经济学、社会学的一些领域中主要研究的正是群体机制型实际因果关系，除了例子3，典型的例子还有获得21年诺贝尔经济学奖的因本斯（Guido Imbens）与他的合作者关注的现象。这些研究的特点是，相应的实际因果关系只有在确定相应的低耦合的机制系统后才明确的，因此这些研究的实质性工作在于获取合适的数据，使用这些数据去确定组件之间的关系，进而推断出相应的因果关系，正是这些研究的这种特点以及这些研究的重要性，使得结构方程模型成为当前实际因果研究的主要形式化模型。

       结构方程模型以及与之类似的形式化方法在群体机制型实际因果研究中发挥着巨大的作用，但是由于个体机制型实际因果中的机制系统是作为整体被探究的，因此对这类实际因果关系，结构方程模型方法很可能仍然会是“英雄无用武之地”，需要发展其他的形式化方法才能应对，由于论文篇幅的限制，我们不再展开。

       最后，使用我们这里得到的分类，可以回应在第二节中提到的对于因果关联项的争论。通常认为，事件是因果关联项，而保罗与一些学者认为，实际因果关系的因果关联项应该是性质实例。在我们的框架下，这两者实际上并不矛盾，在非机制型实际因果中，事件是因果关联项，而在个体机制型实际因果中，性质实例是因果关联项。

六 结束语

       实际因果是一元的还是多元的，是当前因果研究中一个争议的热点。对这个问题以及进而对实际因果分类问题的研究，不仅仅具有理论的意义，对于实践，特别是形式化建模工作也是非常重要的。反过来，已经得到的形式化方法的框架，也提供给我们探讨这一问题的新的视角。费舍尔的多元论观点正是基于结构方程形式模型方法发展出来的。由于使用了形式化方法，费舍尔的工作相对深入而清晰。另一面，上个世纪末兴起的新机制主义认为，实际发生的事件之间由机制勾连着，我们进而论证，机制是结构方程模型的关键要件；但是机制在不同情况里具有不同的地位，由此而来，实际因果的分类将更加复杂，在分析机制的不同作用之后，我们说明实际因果至少可以分类为机制型与非机制型，而在机制型实际因果内部，根据机制系统的耦合程度，又可以分为群体机制性实际因果与个体机制性实际因果，对于这些不同种类的实际因果可能需要不同的形式化方案，特别的，结构方程形式模型方法可能只适合于为群体机制型因果关系建模，由此我们推进了费舍尔的工作。

参考文献

[1] Halpern, Joseph Y. Actual Causality [M]. MIT Press, 2016.

[2] Fischer, Enno. Actual causation[D]. the institute of philosophy at the leibniz university hannover, 2021.

[3] Paul, L. A． Aspect causation[J]. The journal of philosophy，2004，97( 4) : 235 － 256．

[4]刘牧. 解决反事实情境问题的一种新方案[J]. 科学技术哲学研究, 2021, 38(3):7.

[5]Hitchcock, Christopher. Actual causation: What’s the use[A]. In Beebee, Helen, Hitchcock, Christopher, and Price, Huw, editors, Making a Difference[C]. pp. 116–131. Oxford University Press, 2017.

[6] Schaffer, Jonathan. The Metaphysics of Causation[EB/OL]. (2018-08-07)  https://meinong.stanford.edu/entries/causation-metaphysics/

[7] Lewis, David. Causation. The Journal of Philosophy, 70(17):556–567, 1973.

[8] Maudlin, Tim. A modest proposal concerning laws, counterfactuals, and explanation[A]. in The Metaphysics Within Physics[C]. pp.5-49.Clarendon, 2007.

[9] 徐竹. 当代社会科学哲学的因果机制理论述评[J]. 哲学动态, 2012(3):7.

[10] Pearl, Judea. Causality: Models, Reasoning, and Inference [M]. Second Edition, Cambridge University Press, 2009.

[11] Halpern, Joseph. Hitchcock, Christopher. Actual causation and the art of modeling[A]. In Causality, Probability, and Heuristics: A Tribute to Judea Pearl[C]. pp. 383-406.  London: College Publications. 2011.

[12] Hitchcock, Christopher. Causal models [EB/OL]. (2018-08-07) https://plato.stanford.edu/entries/causal-models/.

[13] Fischer, Enno. Three Concepts of Actual Causation[J]. forthcoming in The British Journal for the Philosophy of Science.

[14] 李珍. 反事实与因果机制[J]. 自然辩证法研究, 2009(9):6.

[15] Woodward, James. Mechanisms revisited[J]. Synthese, 2011, 183(3):409-427.

[16] Glennan, Stuart. Mechanisms and the nature of causation[J]. Erkenntnis, 1996.

[17] Hall, Ned. Two concepts of causation[A]. In Collins, John, Hall, Ned, and Paul, L. A., editors, Causation and Counterfactuals[C]. pages 225–276. MIT Press, Cambridge, MA, 2004.

[18] Matthews, Lucas. and Tabery, James. Mechanisms and the metaphysics of causation[A] in The Routledge Handbook of Mechanisms and Mechanical Philosophy [C] . Routledge. pp. 131-143. 2018.

[19] Woodward, James. Making things happen: A theory of causal explanation. New York: Oxford

University Press 2003.

[20] Lewis, David. New work for a theory of universals[J]. Australasian Journal of Philosophy, 1983.

[21]Glennan, Stuart. Illari, Phyllis. The Routledge Handbook of Mechanisms and Mechanical Philosophy[M]. 2017.

[22] Glennan, Stuart. The New Mechanical Philosophy[M], New York: Oxford University Press, 2017.

[23] Machamer, Peter. et al. Thinking about mechanisms [J]. Philosophy of Science, 2000.